Žemiau yra pateikiama glausta informacija apie Pagrindinio Ugdymo Pasiekimų Patikrinimą (PUPP).
PUPP trukmė – 150min.
PAGRINDINĖ SESIJA | 2026 05 13 d. 9h (vykdymo būdas elektroninis)
PAKARTOTINĖ SESIJA | 2026 06 19 d. 9h (vykdymo būdas elektroninis)
Ar reikia būtinai išlaikyti PUPP – dabar numatoma, kad būtina išlaikyti PUPP nuo 2027m. pavasario (kad mokinys būtų perkeltas į III gimnazijos klasę).
PUPP visų galimų taškų suma – 50 taškų (praeitais metais buvo 45 taškai). Užduotį sudaro 30–35 uždaviniai ir (ar) klausimai (praeitais metais buvo 37 uždaviniai). Užduotį sudaro trijų tipų uždaviniai: pasirenkamojo atsakymo – 8–10 uždavinių, kurių teisingas atsakymas vertinamas 1–3 taškais, iš viso 10 taškų, trumpojo atsakymo – 17–19 uždavinių, kurių teisingas atsakymas vertinamas 1–3 taškais, iš viso 25 taškai, pilnojo sprendimo – 5–6 uždaviniai, kurių teisingas sprendimas vertinamas 2–3 taškais, iš viso 15 taškų.
Uždavinių procentinis kiekis pagal žinių lygį: Slenkstinis – 35 proc., patenkinamas – 15 proc., pagrindinis – 35 proc., aukštesnysis – 15 proc.
PUPP pavyzdžiai: 2023 I srautas; 2023 II srautas; 2024 I srautas; 2024 II srautas; 2025 bandomasis; 2025 pagrindinis egzaminas.
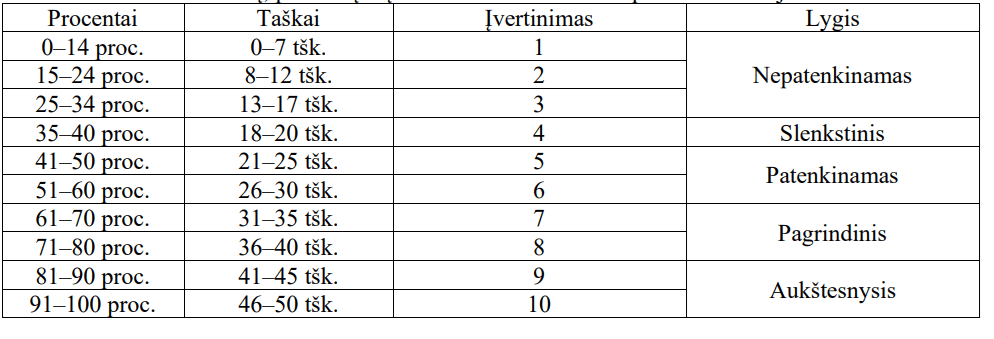
Vertinimo lygiai (pažymiais): Lentelėje yra pateikta taškų konvertavimas į procentus, įvertinimą balais ir užrašymą žodžiais (žinių lygis):
PUPP sudaro trys pagrindinės temos: (Modeliai ir sąryšiai – 55%; Geometrija ir matavimai – 40%; Duomenys ir tikimybės – 5%).
Nuo šių metų per PUPP galima naudotis asmeniniu skaičiuotuvu be tekstinės atminties, t. y. tokiu skaičiuotuvu, kurio klaviatūra neturi viso lotyniškojo raidyno, o skaičiuotuvo ekrane gali būti matomos viena arba dvi eilutės, iš kurių viena skirta veiksmui užrašyti, kita – atsakymui pateikti.
Kokį skaičiuotuvą įsigyti moksleiviui, bei skaičiuotuvų sąrašas, kuriuos galima neštis į PUPP
PUPP formulių lapas: Parsisiųsti PUPP formulių lapą galite paspaudę mygtuką žemiau:
1. MODELIAI IR SĄRYŠIAI
1.1 Dėsningumai
Nagrinėjamos probleminės situacijos, kuomet nustatomas matematinės informacijos trūkumas ir mokomasi ją susirasti, atsirinkti. Sprendžiami uždaviniai, į kuriuos atsakyti galima nevienareikšmiai, kurie turi daugiau negu vieną teisingą atsakymą. Praktikuojamasi sugalvoti naujus klausimus (sąlygą, uždavinį), nustatyti naujo uždavinio ryšį su anksčiau spręstuoju. Sprendžiami uždaviniai, kai skaičius, dydis padalijamas į dvi nelygias dalis, kuriuos sprendžiant reikia remtis proporcingąja dalyba. Nagrinėjama Fibonačio skaičių seka, aukso pjūvio skaičius Φ=(1+sqrt(5))/2, aukso pjūvio seka (0,056; 0,090; 0,146; 0,236; …). Sprendžiami su procentais ir dydžių santykiais susiję uždaviniai: džiovinimo ir drėkinimo; sudėtinių procentų; lydinių, mišinių, tirpalų.
1.2 Algebra
Kvadratinės lygtys. Apibrėžiama antrojo laipsnio (kvadratinė) lygtis. Įrodoma ir taikoma kvadratinės lygties sprendinių formulė. Nagrinėjamos diskriminanto reikšmės sąsajos su kvadratinės lygties sprendinių skaičiumi. Sprendžiami įvairaus konteksto uždaviniai, sudarant kvadratines lygtis.
Raidiniai reiškiniai. Apibrėžiama kvadratinio trinario sąvoka, įrodoma jo skaidymo dauginamaisiais formulė; ji taikoma, sprendžiant uždavinius. Apibrėžiama trupmeninio racionaliojo reiškinio sąvoka, aptariama jo apibrėžimo sritis. Mokomasi pritaikyti žinomus sudėties ir daugybos dėsnius, veiksmų su laipsniais ir trupmenomis savybes, pertvarkant, prastinant nesudėtingus trupmeninius racionaliuosius reiškinius.
Lygčių sistemos. Mokomasi dviejų lygčių sistemas (su dviem nežinomaisiais), kurių viena lygtis pirmojo laipsnio, o kita racionalioji, spręsti grafiniu, keitimo, sudėties, sulyginimo būdais. Nagrinėjamos įvairios realaus pasaulio situacijos, kurios gali būti modeliuojamos lygčių sistemomis.
Racionaliosios lygtys. Apibrėžiama racionaliosios lygties sąvoka. Mokomasi spręsti racionaliąsias lygtis, jas pateikiant pavidalu A(x)/B(x) = 0. Nagrinėjamos įvairios realaus pasaulio ir matematinės situacijos, kurios gali būti modeliuojamos racionaliosiomis lygtimis.
Kvadratinės nelygybės. Apibrėžiama kvadratinės nelygybės sąvoka. Mokomasi kvadratines nelygybes spręsti algebriniu būdu, t. y. kai pradinė kvadratinė nelygybė keičiama dviejų pirmojo laipsnio nelygybių sistemomis. Diskutuojama apie grafinio ir algebrinio būdo taikymo ypatumus, kai šie būdai pasitelkiami kvadratinės funkcijos įvairioms savybėms nagrinėti.
1.3 Tiesiniai ir netiesiniai sąryšiai
Funkcijos samprata. Apibrėžiamos sąvokos: funkcija, funkcijos argumentas, funkcijos reikšmė, funkcijos apibrėžimo sritis, funkcijos reikšmių sritis, funkcijos grafikas. Mokomasi funkciją apibūdinti žodžiais, lentele, grafiku, formule (naudojantis ir skaitmeninėmis priemonėmis), apskaičiuoti ir (ar) nustatyti funkcijos reikšmes, kai yra žinoma funkcijos argumento reikšmė, ir atvirkščiai. Aiškinamasi, kuo funkcijos grafiko eskizas skiriasi nuo grafiko. Mokomasi nustatyti funkcijos apibrėžimo sritį, reikšmių sritį, funkcijos grafiko susikirtimo su koordinačių ašimis taškus; intervalus, kuriuose funkcija įgyja teigiamas ir neigiamas reikšmes; yra didėjančioji, mažėjančioji ar pastovioji.
Tiesinė ir kvadratinė funkcijos. Sprendžiami uždaviniai, kai realaus gyvenimo situacijoms tyrinėti ir modeliuoti – eksperimento duomenims aprašyti – taikomos (pasitelkiamos) funkcijos. Išnagrinėjus tiesinės funkcijos modeliu aprašomus eksperimento duomenis (pavyzdžiui, vaistų dozės poveikis sergantiesiems hipertonine liga po laiko t galėtų būti pavaizduotas žemėjančia tiesės atkarpa), yra apibrėžiama tiesinė funkcija 𝑦=𝑘𝑥+𝑏, tiesės krypties koeficientas k, postūmio koeficientas b. Braižant konkrečių tiesinių funkcijų grafikų eskizus (tieses), tyrinėjama, kaip tiesės padėtis priklauso nuo šių koeficientų reikšmių. Išnagrinėjus kvadratine funkcija aprašomus eksperimento duomenis, įvedama kvadratinė funkcijos 𝑦=𝑎𝑥^2+𝑏𝑥+𝑐; y=ax^2+bx+c, kai a ≠ 0, sąvoka, braižomi jos grafiko (parabolės) eskizai. Tyrinėjama, kaip parabolės padėtis priklauso nuo a ir 𝐷=𝑏^2−4𝑎𝑐 reikšmių. Naudojantis skaitmeninėmis priemonėmis, tyrinėjama, kaip, taikant transformacijas, iš funkcijos 𝑦=𝑥 grafiko gauti funkcijos 𝑦=𝑘𝑥+𝑏 grafiką, o iš funkcijos 𝑦=𝑥^2 grafiko gauti funkcijos y=a(x−m)^2+n grafiką. Sprendžiami uždaviniai, kuriuose įvairios realaus pasaulio situacijos yra modeliuojamos funkcijomis: 𝑦=𝑘𝑥+𝑏, 𝑦=𝑎𝑥^2+𝑏𝑥+c, 𝑦=𝑎(𝑥−𝑚)^2+𝑛, 𝑦=𝑎(𝑥−𝑥1)(𝑥−𝑥2).
2. GEOMETRIJA IR MATAVIMAI
2.1 Figūros
Plokščiosios figūros. Apibrėžiami centrinis ir įbrėžtinis kampai. Nagrinėjamos kampų savybės apie įbrėžtinius kampus bei centrinį ir įbrėžtinį kampus, kurie kerta tą patį lanką. Apibrėžiamos sąvokos: apskritimo liestinė, kirstinė, styga; skritulio išpjova, nuopjova. Paaiškinama, kad apskritimo lankas matuojamas ne tik ilgio matavimo vienetais, bet ir laipsniais. Aptariamos ir taikomos savybės: liestinės statmenumo spinduliui, susikertančiųjų liestinių atkarpų iki lietimosi su apskritimu taškų, susikertančiųjų stygų. Mokomasi remtis apibrėžimais ir įrodytais teiginiais, sprendžiant įvairius matematinio ir realaus konteksto uždavinius, įrodinėjant kitus teiginius.
Nagrinėjant panašiųjų figūrų perimetrus, plotus, nustatomas dėsningumas, jis pagrindžiamas ir taikomas, sprendžiant uždavinius. Tyrinėjamos ir pagrindžiamos trikampio pusiaukampinių, pusiaukraštinių savybės. Apibrėžiamos sąvokos: įbrėžtinis daugiakampis, apibrėžtinis daugiakampis. Suformuluojami ir pagrindžiami teiginiai apie į trikampį įbrėžto apskritimo ir apie trikampį apibrėžto apskritimo centrus. Mokomasi taikyti formules 𝑆=𝑟𝑝, 𝑆=(𝑎𝑏𝑐)/4𝑅. Mokomasi pagrįsti ir taikyti įbrėžtinio ir apibrėžtinio keturkampio savybes. Mokomasi remtis apibrėžimais ir įrodytais teiginiais, sprendžiant įvairius matematinio ir realaus konteksto uždavinius, įrodinėjant kitus teiginius.
3. DUOMENYS IR TIKIMYBĖS
3.1 Statistika
3.2 Tikimybių teorija
Sudaryti kelių elementų rinkinius, kai jų elementai imami iš skirtingų arba iš vienos aibės. Tiesiogiai apskaičiuoti rinkinių variantų skaičių, kai elementų tvarka rinkinyje yra svarbi arba nesvarbi, taikyti daugybos taisyklę apskaičiuojant rinkinių variantų skaičių tik, kai elementų tvarka rinkinyje svarbi. Paprasčiausiais atvejais užrašyti bandymo baigčių aibę ir įvykiui palankių baigčių aibę, rasti baigčių skaičių. Daryti paprasčiausias išvadas apie baigties tikėtinumą.
Aptariama, kas yra kelių elementų rinkinys, kaip užrašoma tokių rinkinių aibė. Mokomasi sudaryti rinkinius, kai elementai imami iš tos pačios aibės ar skirtingų aibių. Nagrinėjami pavyzdžiai, kai elementų tvarka rinkinyje svarbi ir kai nesvarbi. Aiškinamasi, kaip apskaičiuoti rinkinių variantų skaičių, atsižvelgiant į elementų tvarkos rinkinyje svarbą. Aptariama, kada, skaičiuojant rinkinių variantų skaičių, patogu naudotis kombinatorikos sudėties ir daugybos taisyklėmis. Rinkinių sudarymo įgūdžiai taikomi, sprendžiant tikimybių uždavinius. Mokomasi įvertinti atsitiktinio įvykio tikimybę, renkant duomenis apie atsitiktinį procesą ir stebint jo ilgalaikį santykinį dažnį bei gautą rezultatą, palyginant su teorine šio įvykio tikimybe (pavyzdžiui, šešiasienio kauliuko ridenimas iki 600 kartų ir kauliuko atvirtimo šešiomis akutėmis stebėjimas).
Kontroliniai darbai –> suskirstyta pagal temas.
